Recent lecture on Mahout for SDForum

I gave a lecture last night on recent additions to Mahout.

The slides are here: http://www.slideshare.net/tdunning/sdforum-11042010

I can amplify this post with answers to any questions that anybody puts in the comments.

Mahout 0.4 released!

Go to the Apache Mahout site for more info.  Here is the official announcement:

We are pleased to announce release 0.4 of Mahout. Virtually every corner of the project has changed, and significantly, since 0.3. Developers are invited to use and depend on version 0.4 even as yet more change is to be expected before the next release. Highlights include:

- Model refactoring and CLI changes to improve integration and consistency

- New ClusterEvaluator and CDbwClusterEvaluator offer new ways to evaluate clustering effectiveness

- New Spectral Clustering and MinHash Clustering (still experimental)

- New VectorModelClassifier allows any set of clusters to be used for classification

- Map/Reduce job to compute the pairwise similarities of the rows of a matrix using a customizable similarity measure

- Map/Reduce job to compute the item-item-similarities for item-based collaborative filtering

- RecommenderJob has been evolved to a fully distributed item-based recommender

- Distributed Lanczos SVD implementation

- More support for distributed operations on very large matrices

- Easier access to Mahout operations via the command line

- New HMM based sequence classification from GSoC (currently as sequential version only and still experimental)

- Sequential logistic regression training framework

- New SGD classifier

- Experimental new type of NB classifier, and feature reduction options for existing one

- New vector encoding framework for high speed vectorization without a pre-built dictionary

- Additional elements of supervised model evaluation framework

- Promoted several pieces of old Colt framework to tested status (QR decomposition, in particular)

- Can now save random forests and use it to classify new data

- Many, many small fixes, improvements, refactorings and cleanup

Details on what's included can be found in the release notes.

Downloads are available from the Apache Mirrors

New Mahout release coming

The vote has started for the 0.4 Mahout release.  Lots of new stuff, but the part that I am excited about is a fairly comprehensive implementation of logistic regression suitable for large scale training and high speed classification, but there is a whole lot more.

With the 0.4 release, Mahout is moving along strongly towards the fabled 1.0 release.  At that point, we will start paying lots of attention to backwards compatibility.  That will be good, but the current wild and wooly policy is pretty handy if you have something in mind that Mahout really, really needs because we can get new things in pretty readily right now.

See http://mahout.apache.org/ for the release when it arrives and watch my twitter feed for an announcement.

Why is the sum of two uniform randoms not uniform?

Lance Norkog asks on the Mahout mailing list why adding two uniformly distributed random variables gives a pyramidal distributed value. I would normally answer on the mailing list, but here I can use lovely math notation. As I mentioned on-list, this is a very basic result that is related to the law of large numbers.

If we were to draw a picture of the joint distribution of these variables \(x\) and \(y\), we would get something that is 1 inside the \([0,1] \times [0,1]\) square and 0 outside that region.

For a given value \(\alpha\) of the sum \(x + y\), there is a diagonal line segment where \(x+y=\alpha\) and \(x\) and \(y\) are in the square. Where \(z \le 0\) or \(z \ge 2\) that intersection vanishes and for \(0 \lt z \lt 2\), that intersection varies in length. The probability of the sum having some particular value z is proportional to the length of that intersection. As you can imagine, the intersection varies in size linearly and it reaches a maximum where z = 1.

For the sum of three random variables, the situation is more complex to reason about geometrically because we need to worry about the intersection of a plane and a cube.  For more variables, the geometry is not worth the trouble.

If we tackle the problem a bit more rigorously, then the easiest way to approach the problem is to compute the cumulative distribution of various values of sums. That leads to a convolution integral over the density functions involved. Since the densities are all 1, the integration limits are the key to the value and those limits have to broken down into cases. Actually doing these integrals is a pretty rare activity since the limit is approximated so well after just a few iterations.

Just how quickly that convergence happens is can be seen by looking at the empirical distribution of the sum of three uniform deviates.  I used something very like this R code to produce the graph below:


   hist(runif(100000)+runif(100000)+runif(100000), 
        breaks=50, prob=T)
   lines(seq(-1,4,by=0.01), dnorm(seq(-1,4,by=0.01), 
        1.5, sqrt(1/4)))


In this graph, the red curve is the normal distribution with the same mean and standard deviation.  As you can see, the peak is a tiny bit too high and the tails are just a skoshi too long for the normal to be a good description of the samples of the sum.   

This is, however, just the sum of three random values.  If you sum more values, the convergence to the normal distribution is very strong and by the time you are adding six uniform random values together, the difference between the distributions is no longer visible in a graph like this and can only be detected numerically using lots of data and clever things like a Kolmogorov-Smirnov test.

The moral here is that there isn't much way to avoid this regression to the normal distribution and distorting the data to avoid it is probably pointless.

But if you are like me, being just a little more normal always made it easier to get along.

Sadder things

I spent this last weekend holding a hand that grew cold in the early hours of Sunday morning.

That hand helped me through much of my life.  No longer.  At least not in the flesh.

Nobody who reads this blog is likely to have known my father and given how little he talked about things he had done, few who knew him would know much of the many things he did.  He lived a long life and a full one.  Along the way he saw things few will ever see.

In his prime, he was simply extraordinary.  He could see and he could hear better than anyone I have ever known. That could be torture, as it was the time when a cat walking in the next room woke him from a deep sleep but it was what let him fly the way he did.  And fly he did in planes large and small.  He checked out Gary Powers in the U-2, flew P-47's and P-38 in combat and flew with me in small aircraft.  We fished and walked and camped across the western US and we lived in many places.

He didn't show off his mental abilities, but there too he could do things few others could match.  He passed a graduate reading exam in French without ever studying any romance language.  I saw him on several occasions understand spoken German also without having studied the language.  He spoke of the shape and rate of physical processes in ways that only somebody with innate ability in math could possibly do.

These faculties declined in age as they must with all of us, but even thus dimmed his candle burned bright.

But it did not last.  I saw it sputter and fade.  Then, between one instant and the next, it was gone.

Word Count using Plume

Plume is working for toy programs!

You can get the source code at http://github.com/tdunning/Plume

Here is a quick description of how to code up the perennial map-reduce demo program for counting words.  The idea is that we have lines of text that we have to tokenize and then count the words.  This example is to be found in the class WordCountTest in Plume.

So we start with PCollection lines for input.  For each line, we split the line
into words and emit them as a separate record:

    
  PCollection words = lines
    .map(new DoFn() {
      @Override
      public void process(String x, EmitFn emitter) {
        for (String word : onNonWordChar.split(x)) {
          emitter.emit(word);
        }
      }
    }, collectionOf(strings()));


Then we emit each word as a key for a PTable with a count of 1.  This is just the same as most word-count implementations except that we have separated the tokenization from the emission of the original counts.  We could have put them together into a single map operation, but the optimizer will do that for us (when it exists) so keeping the functions modular is probably better.


  PTable wc = words
    .map(new DoFn>() {
      @Override
      public void process(String x, 
                         EmitFn> emitter) {
         emitter.emit(Pair.create(x, 1));
      }
    }, tableOf(strings(), integers()))


Then we group by word


  .groupByKey()


And do the counting.  Note how we don't have to worry about the details of using a combiner or a reducer.


  .combine(new CombinerFn() {
     @Override
     public Integer combine(Iterable counts) {
       int sum = 0;
       for (Integer k : counts) {
         sum += k;
       }
       return sum;
     }
   });

In all, it takes 27 lines to implement a slightly more general word-count than the one in the Hadoop tutorial.  If we were compare apples to apples, this could would probably be a few lines shorter.  The original word-count demo was 210 lines to do the same thing.

The new grool

A few years ago, I built a prototype system I called grool in Groovy to simplify map-reduce programming.  My goal was to use Groovy to handle control flow and define operations but to execute large programs using Hadoop.

Grool foundered on the difficulty in transporting closures over the network.  I used a clever trick to avoid the problem, but it depended on the ability to execute a script multiple times with different meanings each time.  That is a difficult concept to convey to users and the result was that grool really didn't work that well for ordinary folks to use.

A bit later, the guys at Google developed FlumeJava which has many of the same goals and many of the same benefits as grool intended to provide.  In Java, however, transporting functional objects it paradoxically much simpler than in Groovy.  The difference is entirely because Java is statically compiled and thus state-less functional classes can be referred to by name in different JVM's with access to the same jar.

Flume also provide an optimizer which is made possible because Flume uses lazy evaluation.   This makes FlumeJava programs nearly as efficient as well-optimized hand-written programs.  Other systems like Pig and Cascading are able to re-write their logical plan, but Pig especially has problems because it has no real access to a Turing complete language.

In addition, Flume has some interesting choices in terms of API.

All in all, Flume-like systems are definitely worth playing with.  In order to make that easier, I just implemented an eager, sequential version of an approximate clone of FlumeJava that I call Plume.  The name is a presumptuous one, anticipating that if all goes well, we would be able to build a community and bring Plume into Apache where it would be Apache Plume.  There it would provide some redress for the clear fauna bias in software names.

Check it out at http://wiki.github.com/tdunning/Plume/

Hadoop user group AKA Mahout Users Anonymous

At the Hadoop User Group meeting last evening it was quite the Mahout love fest.  First the Yahoo team described their spam fighting efforts which apparently are partially anchored by frequent item set mining using Mahout (thanks to Robin Anil's hard work as a GSoC student).  Then later Ken Krugler demonstrated some of what you can do with web-mining and Mahout.

These are just two of a growing number of real-world uses of Mahout which is really beginning to grow up.  Related to that growing up, the Apache board just decided to make Mahout a top level project.  That will take a little while to make real, but the first steps are already happening.

You can find out more about how Mahout is being used by perusing the Mahout wiki.

Slide decks available here for the HUG presentations.

Interview on Mahout available

I just had an interchange with Gilad Manor of InfoQ (as did Grant).  The results are to be found in the article on Mahout status that resulted.

Sampling a Dirichlet Distribution (revised)

Last year, I casually wrote a post about how to sample from a prior for Dirichlet distributions.  There were recently a few comments on this blog and it now occurs to me that there is a massive simplification that is possible for the problem.

What I suggested back then was to sample the parameters of a Dirichlet distribution by sampling from a Dirichlet distribution and then multiplying that by a magnitude sampled from an exponential distribution.  As it turns out, this is a special case of a much nicer general method.

The new method is to sample each parameter independently from a gamma distribution
\[\gamma_i \sim \mathrm{Gamma}(\alpha_i, \beta_i) \]
This can be related to my previous method where we had the parameters expressed as a magnitude \(\alpha\) multiplied by a vector \(\vec m\) whose components sum to 1. Expressed in terms of the new method
\[\alpha = \sum_i \gamma_i \]
and
\[ m_i = \gamma_i / \alpha \]
Moreover, if all of the \(\beta_i\) are equal, then \(\alpha\) is gamma distributed with shape parameter \(\sum_i \alpha_i\). If this sum is 1, then we have an exponential distribution for \(\alpha\) as in the original method.

I am pretty sure that this formulation also makes MCMC sampling from the posterior distribution easier as well because the products inside the expression for the joint probability will get glued together in a propitious fashion.

Sampling Dirichlet Distributions (chapter 2-b)

In the previous post, I talked about how sampling in soft-max space can make Metropolis algorithms work better for Dirichlet distributions. Here are some pictures that show why. These pictures are of three parameter Dirichlet distributions with the simplex projected into two dimensions. Dirichlet distributions with different parameters can look like this:

or this

or this

These were all generated using the standard algorithm for sampling from a Dirichlet distribution.


In R, that algorithm is this

rdirichlet = function(n, alpha) {
  k = length(alpha)
  r = matrix(0, nrow=n, ncol=k)
  for (i in 1:k) {
    r[,i] = rgamma(n, alpha[i], 1)
  }
  r = matrix(mapply(function(r, s) {return (r/s)}, r, rowSums(r)), ncol=k)
  return (r)
}

That is, first sample $(y_1 \ldots y_n)$  using a gamma distribution
\[y_i \sim \mathrm {Gamma} (\alpha_i, 1)\]
Then normalize to get the desired sample
\[\pi_i = {y_i \over \sum_j y_j}\]
In contrast, here are 30,000 samples computed using a simple Metropolis algorithm to draw samples from a Dirichlet distribution with $\alpha = (1,1,1)$ .  This should give a completely uniform impression but there is noticeable thinning in the corners where the acceptance rate of the sampling process drops.

The thinning is only apparent.  In fact, what happens is that the samples in the corners are repeated, but that doesn't show up in this visual presentation.  Thus the algorithm is correct, but it exhibits very different mixing behavior depending on where you look.

A particularly unfortunate aspect of this problem is that decreasing the size of the step distribution in order to increase the acceptance rate in the corners makes the sampler take much longer to traverse the region of interest and thus only partially helps the problem.  Much of the problem is that when we have reached a point near the edge of the simplex or especially in a corner, many candidate steps will be off the simplex entirely and will thus be rejected.  When many parameters are small, this is particularly a problem because steps that are not rejected due to being off the simplex are likely to be rejected because the probability density drops dramatically as we leave the edge of the simplex.  Both of these problems become much, much worse in higher dimensions.

A much better alternative is to generate candidate points in soft-max space using a Gaussian step distribution.  This gives us a symmetric candidate distribution that takes small steps near the edges and corners of the simplex and larger steps in the middle of the range.  The sensitivity to the average step size (in soft-max space) is noticeably decreased and the chance of stepping out of the simplex is eliminated entirely.

This small cleverness leads to the solution of the question posed in a comment some time ago by Andrei about how to sample from the posterior distribution where we observe counts sampled from a multinomial
\[\vec k \sim \mathrm {Multi} (\vec x)\]
where that multinomial has a prior distribution defined by
\[\begin{aligned}
\vec x &= \alpha \vec m \\
\alpha &\sim \mathrm{Exp} (\beta_0) \\
\vec m &\sim \mathrm{Dir} (\beta_1 \ldots \beta_n)
\end{aligned}\]
More about that in my next post.

Sampling Dirichlet Distributions (chapter 2-a)

In a previous post on sampling from Dirichlet distributions that related to a comment by Andrew Gelman on the same topic I talked a bit about how to sample the parameters of a Dirichlet (as opposed to sampling from a Dirichlet distribution with known parameters).

In responding to some questions and comments on my post, I went back and reread Andrew's thoughts and think that they should be amplified a bit.

Basically, what Andrew suggested is that when sampling from a Dirichlet, it is much easier to not sample from Dirichlet at all, but rather to sample from some unbounded distribution and then reduce that sample back to the unit simplex. The transformation that Andrew suggested is the same as the so-called soft-max basis that David Mackay also advocates for several purposes. This method is not well know, however, so it deserves a few more pixels.

The idea is that to sample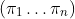 from some distribution you instead sample



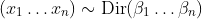
and then reduce to the sample you want



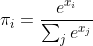
Clearly this gives you values on the unit simplex. What is not clear is that this distribution is anything that you want. In fact, if your original sample is from a normal distribution



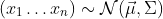
then you can come pretty close to whatever desired Dirichlet distribution you like. More importantly in practice, this idea of normally sampling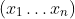 and then transforming gives a very nice prior serves as well as a real Dirichlet distribution in many applications.

Where this comes in wonderfully handy is in MCMC sampling where you don't really want to sample from the prior, but instead want to sample from the posterior. It isn't all that hard to use the Dirichlet distribution directly in these cases, but the results are likely to surprise you. For instance, if you take the trivial case of picking a uniformly distributed point on the simplex and then jumping around using Metropolis updates based on a Dirichlet distribution, you will definitely have the right distribution for your samples after just a bit of sampling. But if you plot those points, they won't look at all right if you are sampling from a distribution that has any significant density next to the boundaries of the simplex. What is happening is that the high probability of points near the boundaries is accounted for in the Metropolis algorithm by having a high probability of rejecting any jump if you are near the boundary. Thus, the samples near the boundary are actually repeated many times leading to the visual impression of low density where there should be high density.

On the other hand, if you were to do the Metropolis jumps in the soft-max basis, the problem is entirely avoided because there are no boundaries in soft-max space. You can even use the soft-max basis for the sole purpose of generating candidate points and do all probability calculations in terms on the simplex.

In my next post, I will provide a concrete example and even include some pictures.

Big Data and Big Problems

In talks recently, I have mentioned an ACM paper that showed just how bad random access to various storage devices can be.  About half the time I mention this paper, somebody asks for the reference which I never know off the top of my head.  So here it is

The Pathologies of Big Data

Of course, the big deal is not that disks are faster when read sequentially.  We all know that and most people I talk to know that the problem is worse than you would think.  The news is that random access to memory is much, much worse than most people would imagine.  In the slightly contrived example in this paper, for instance, sequential reads from a hard disk deliver data faster than randomized reads from RAM.  That is truly horrifying.

Even though you can pick holes in the example, it shows by mere existence that the problem of random access is much worse than almost anybody has actually internalized.

Nice package of software an tutorials for corpus analysis

I was about to try to provide some help in using the \(G^2\) implementations that I use and give away for a graduate student trying to do some corpus analysis and I found this lovely site describing how to do corpus analysis using R.   Marco Baroni and Stefan Evert have done a really lovely job there of describing how to do a large number of simple tasks.  Kudos to them!

For not necessarily the most noble reasons, I was happy to see from their slide show on computing association measures that \(G^2\) is still essentially on top as a measure of association after all of these years.